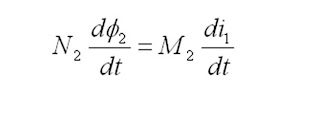Induktansi

Sebelum kita membahas tentang induktansi, ada baiknya kita mempelajari tentang konsep fluks. Sebuah toroida dengan N lilitan dialiri arus I sehingga menimbulkan fluks total ϕ. Fluks total linkage didefinisikan sebagai jumlah perkalian dari lilitan dan fluks ϕ yang bertautan dengan masing-masing lilitan.

Sekarang kita definisikan induktansi atau induktansi diri sebagai hasil bagi fluks total dengan arus I. Arus total I yang mengalir dalam kumparan N menimbulkan ϕ dan pertautan fluks Nϕ, disini kita anggap fluks bertautan dengan masing-masing lilitan. Induktansi dilambangkan dengan L dengan satuan Henry.

L = Nϕ / I ................................. (1)

Dimana:

ϕ = Jumlah fluks yang menembus setiap permukaan yang kelilingnya ialah setiap lintasan yang berimpit dengan salah satu lintasan N.

Persamaan (1) dapat dipakai untuk menghitung induktansi parameter sebuah kabel sesumbu y yang berjari-jari dalam a dan jejari luar b. Sehingga akan kita dapatkan persamaan sebagai berikut:

Dan kita peroleh induktansi untuk panjang d:

1. Induktansi Diri

Merupakan induktansi dimana GGL induksi diri yang terjadi di dalam suatu penghantar bila kuat arusnya berubah-ubah dengan satuan kuat arus tiap detik. Arus induktansi diri yang timbul pada sebuah trafo atau kumparan yang dapat menimbulkan GGL induksi yang besarnya berbanding lurus dengan cepat perubahan kuat arusnya. Hubungan dengan GGL induksi diri dengan laju perubahan kuat arus dirumuskan Joseph Henry sebagai berikut:

Gaya Gerak Listrik ialah energi permuatan yang dibutuhkan untuk mengalirkan arus dalam loop kawat. Dari rumus diatas dapat didefinisikan sebagai berikut: suatu kumparan mempunyai induktansi diri sebesar 1 H bila perubahan arus listrik sebesar 1 A dalam 1 detik pada kumparan tersebut menimbulkan GGL induksi sendiri sebesar 1 volt. (Buku Fisika SMU kelas 2, hal 90)

2. Induksi Diri Sebuah Kumparan

Perubahan arus dalam kumparan ditentukan oleh perubahan fluks magnetik 0 dalam kumparan. Besarnya induksi diri dari suatu kumparan ialah:

3. Induktansi diri Solenoida dan Toroida

Besarnya induktansi solenoida dan toroida dapat kita ketahui dengan menggunakan persamaan berikut:

4. Induktansi Bersama

Satuan SI dari induktansi bersama dapat dinamakan henry (H), untuk menghormati fisikawan Amerika Joseph Henry (1797-1878), salah seorang dari penemu induksi elektromagnetik. Satu henry (1 H) sama dengan satu weber per ampere (1 Wb/A).

Induktansi bersama dapat merupakan sebuah gangguan dalam rangkaian listrik karena perubahan arus dalam satu rangkaian dapat menginduksi tge yang tidak diingikan oleh rangkaian lainnya yang berada didekatnya. Untuk meminimalkan efek ini, maka sistem rangkaian ganda harus dirancang dengan M adalah sekecil-kecilnya; misalnya, dua koil akan ditempatkan jauh terpisah terhadap satu sama lain atau dengan menempatkan bidang-bidang kedua koil itu tegak lurus satu sama lain. Induktansi bersama juga mempunyai banyak pemakaian, contohnya transformator, yang dapat digunakan dalam rangkaian arus bolak-balik untuk menaikan atau menurunkan tegangan. Sebuah arus bolak-balik yang berubah terhadap waktu dalam satu koil pada transformator itu menghasilkan arus bolak-balik dalam koil lainnya; nilai M, yang tergantung pada geometri koil-koil, menentukan amplitudo dari tge induksi dalam koil kedua dan karena itu maka akan menginduksi amplitudo tegangan keluaran tersebut.

Definisi induktansi bersama dapat dilihat dari persamaan berikut:

N₂ϕ₂ ialah banyaknya tautan fluksi dengan kumparan 2. Jika bahan feromagnetik tidak ada, maka fluks ϕ₂ berbanding langsung dengan arus I dan induktansi mutualnya konstan, tak bergantung pada I₁. (Buku Rangkaian Listrik, hal 178)

Jika arus tersebut berubah terhadap waktu, maka:

Ruas kiri persamaan ini adalah harga negatif GGL induksi ε₂ dalam kumparan 2, sehingga:

Berdasarkan sudut pandang ini, induktansi mutual dapat dianggap ggl induksi dalam kumparan 2.

Jangka Sorong

Jangka sorong adalah suatu alat ukur panjang yang dapat dipergunakan untuk mengukur panjang suatu benda dengan ketelitian hingga 0,1 mm. keuntungan penggunaan jangka sorong adalah dapat dipergunakan untuk mengukur diameter sebuah kelereng, diameter dalam sebuah tabung atau cincin, maupun kedalam sebuah tabung.

Pada gambar disamping ditunjukkan bagian-bagian dari jangka sorong. (sorot masing-masing bagian dari jangka sorong tersebut untuk mengetahui nama setiap bagian).

Secara umum, jangka sorong terdiri atas 2 bagian yaitu rahang tetap dan rahang geser. Jangka sorong juga terdiri atas 2 bagian yaitu skala utama yang terdapat pada rahang tetap dan skala nonius (vernier) yang terdapat pada rahang geser.

Sepuluh skala utama memiliki panjang 1 cm, dengan kata lain jarak 2 skala utama yang saling berdekatan adalah 0,1 cm. Sedangkan sepuluh skala nonius memiliki panjang 0,9 cm, dengan kata lain jarak 2 skala nonius yang saling berdekatan adalah 0,09 cm. Jadi beda satu skala utama dengan satu skala nonius adalah 0,1 cm – 0,09 cm = 0,01 cm atau 0,1 mm. Sehingga skala terkecil dari jangka sorong adalah 0,1 mm atau 0,01 cm.

Ketelitian dari jangka sorong adalah setengah dari skala terkecil. Jadi ketelitian jangka sorong adalah : Dx = ½ x 0,01 cm = 0,005 cm.
Dengan ketelitian 0,005 cm, maka jangka sorong dapat dipergunakan untuk mengukur diameter sebuah kelereng atau cincin dengan lebih teliti (akurat).

Seperti yang sudah dijelaskan sebelumnya bahwa jangka sorong dapat dipergunakan untuk mengukur diameter luar sebuah kelereng, diameter dalam sebuah tabung atau cincin maupun untuk mengukur kedalaman sebuah tabung. Berikut akan dijelaskan langkah-langkah menggunakan jangka sorong untuk keperluan tersebut


1. Mengukur diameter luar

Untuk mengukur diameter luar sebuah benda (misalnya kelereng) dapat dilakukan dengan langkah sebagai berikut
* Geserlah rahang geser jangka sorong kekanan sehingga benda yang diukur dapat masuk
diantara kedua rahang (antara rahang geser dan rahang tetap)
* Letakkan benda yang akan diukur diantara kedua rahang.
* Geserlah rahang geser kekiri sedemikian sehingga benda yang diukur terjepit oleh kedua
rahang
* Catatlah hasil pengukuran anda


2. Mengukur diameter dalam

Untuk mengukur diameter dalam sebuah benda (misalnya diameter dalam sebuah cincin) dapat dilakukan dengan langkah sebagai berikut :

*Geserlah rahang geser jangka sorong sedikit kekanan.
* Letakkan benda/cincin yang akan diukur sedemikian sehingga kedua rahang jangka sorong
masuk ke dalam benda/cincin tersebut
* Geserlah rahang geser kekanan sedemikian sehingga kedua rahang jangka sorong menyentuh
kedua dinding dalam benda/cincin yang diukur
* Catatlah hasil pengukuran anda


3. Mengukur kedalaman

Untuk mengukur kedalaman sebuah benda/tabung dapat dilakukan dengan langkah sebagai berikut :

* Letakkan tabung yang akan diukur dalam posisi berdiri tegak.
* Putar jangka (posisi tegak) kemudian letakkan ujung jangka sorong ke permukaan tabung
yang akan diukur dalamnya.
* Geserlah rahang geser kebawah sehingga ujung batang pada jangka sorong menyentuh dasar
tabung.
* Catatlah hasil pengukuran anda.


Untuk membaca hasil pengukuran menggunakan jangka sorong dapat dilakukan dengan langkah sebagai berikut :

1. Bacalah skala utama yang berimpit atau skala terdekat tepat didepan titik nol skala nonis.
2. Bacalah skala nonius yang tepat berimpit dengan skala utama.
3. Hasil pengukuran dinyatakan dengan persamaan :

Hasil = Skala Utama + (skala nonius yang berimpit x skala terkecil jangka sorong) = Skala Utama + (skala nonius yang berimpit x 0,01 cm)

Karena Dx = 0,005 cm (tiga desimal), maka hasil pembacaan pengukuran (xo) harus juga dinyatakan dalam 3 desimal. Tidak seperti mistar, pada jangka sorong yang memiliki skala nonius, Anda tidak pernah menaksir angka terakhir (desimal ke-3) sehingga anda cukup berikan nilai 0 untuk desimal ke-3. sehingga hasil pengukuran menggunakan jangka sorong dapat anda laporkan sebagai :

Panjang L = xo ¬+ Dx

Misalnya L = (4,990 + 0,005) cm

Jangka sorong biasanya digunakan untuk:

1. Mengukur suatu benda dari sisi luar dengan cara diapit;
2. Mengukur sisi dalam suatu benda yang biasanya berupa lubang (pada pipa, maupun
lainnya) dengan cara diulur;
3. Mengukur kedalamanan celah/lubang pada suatu benda dengan cara
“menancapkan/menusukkan” bagian pengukur.
4. Jangka sorong memiliki dua macam skala: skala utama dan nonius.





Lihatlah skala nonius yang berhimpit dengan skala utama. Di contoh, yang berhimpit adalah angka 7 (diberi tanda merah). Itu berarti 0.07 mm. Sekarang lihatlah ke skala utama di sebelah kiri angka nonius 0. Di situ menunjukkan angka 2,4 cm. Berarti hasil pengukurannya adalah 2,4 cm + 0.07 cm = 2,47 cm. Ingat lagi kan pelajaran SMA? Hehe. Untuk pembacaan ke inch prinsipnya sama, hanya saja harus pintar menggunakan skala yang berbeda

Komputer Kuantum Komputer Masa Depan

Teknologi komputer merupakan salah satu teknologi yang paling cepat mengalami perkembangan dan kemajuan. Komputer-komputer yang ada saat ini sudah mencapai kemampuan yang sangat mengagumkan. Tetapi kedahsyatan komputer tercanggih yang ada saat ini pun masih belum bisa memuaskan keinginan manusia yang bermimpi untuk membuat sebuah Supercomputer yang benar-benar memiliki kecepatan super. Komputer yang nantinya layak untuk benar-benar disebut sebagai Komputer Super ini adalah Komputer Kuantum. Teori tentang komputer kuantum ini pertama kali dicetuskan oleh fisikawan dari Argonne National Laboratory sekitar 20 tahun lalu. Paul Benioff merupakan orang pertama yang mengaplikasikan teori fisika kuantum pada dunia komputer di tahun 1981.

Komputer yang biasa kita gunakan sehari-hari merupakan komputer digital. Komputer digital sangat berbeda dengan komputer kuantum yang super itu. Komputer digital bekerja dengan bantuan microprocessor yang berbentuk chip kecil yang tersusun dari banyak transistor. Microprocessor biasanya lebih dikenal dengan istilah Central Processing Unit (CPU) dan merupakan ‘jantung’nya komputer. Microprocessor yang pertama adalah Intel 4004 yang diperkenalkan pada tahun 1971. Komputer pertama ini cuma bisa melakukan perhitungan penjumlahan dan pengurangan saja. Memory komputer menggunakan sistem binary atau sistem angka basis 2 (0 dan 1) yang dikenal sebagai BIT (singkatan dari Binary digIT). Konversi dari angka desimal yang biasa kita gunakan (angka berbasis 10 yang memiliki nilai 0 sampai 9) adalah sebagai berikut:

0 = 0

1 = 1

2 = 10

3 = 11

4 = 100

5 = 101

6 = 110

7 = 111

8 = 1000

9 = 1001

10 = 1010

11 = 1011

12 = 1100

13 = 1101

14 = 1110

15 = 1111

16 = 10000

17 = 10001

Kalau kita ingin menghitung angka apa yang dilambangkan oleh 101001 caranya sebagai berikut (menggunakan sistem 2n):

(1 x 25) + (0 x 24) + (1 x 23) + (0 x 22) + (0 x 21) + (1 x 20) = 32 + 0 + 8 + 0 + 0 +1 = 41.

Contoh perhitungan penjumlahan matematika menggunakan sistem binary:

10 1010

23 + 10111 +

33 100001

Sistem inilah yang selama ini kita gunakan saat kita mengolah informasi menggunakan komputer. Quantum Computer atau komputer kuantum memanfaatkan fenomena ‘aneh’ yang disebut sebagai superposisi. Dalam mekanika kuantum, suatu partikel bisa berada dalam dua keadaan sekaligus. Inilah yang disebut keadaan superposisi. Dalam komputer kuantum, selain 0 dan 1 dikenal pula superposisi dari keduanya. Ini berarti keadaannya bisa berupa 0 dan 1, bukan hanya 0 atau 1 seperti di komputer digital biasa. Komputer kuantum tidak menggunakan Bits tetapi QUBITS (Quantum Bits). Karena kemampuannya untuk berada di bermacam keadaan (multiple states), komputer kuantum memiliki potensi untuk melaksanakan berbagai perhitungan secara simultan sehingga jauh lebih cepat dari komputer digital.

Komputer kuantum menggunakan partikel yang bisa berada dalam dua keadaan sekaligus, misalnya atom-atom yang pada saat yang sama berada dalam keadaan tereksitasi dan tidak tereksitasi, atau foton (partikel cahaya) yang berada di dua tempat berbeda pada saat bersamaan. Apa maksudnya ini?

Atom memiliki konfigurasi spin. Spin atom bisa ke atas (up), bisa pula ke bawah (down). Misalnya saat spin atom mengarah ke atas (up) kita beri lambang 1, sedangkan spin down adalah 0 (seperti dalam sistem binary di komputer digital). Atom-atom berada dalam keadaan superposisi (memiliki spin up dan down secara bersamaan) sampai kita melakukan pengukuran. Tindakan pengukuran memaksa atom untuk ‘memilih’ salah satu dari kedua kemungkinan itu. Ini berarti sesudah kita melakukan pengukuran, atom tidak lagi berada dalam keadaan superposisi. Atom yang sudah mengalami pengukuran memiliki spin yang tetap: up atau down.

Saat konsep ini diterapkan dalam komputer kuantum, keadaan superposisi terjadi pada saat proses perhitungan sedang berlangsung. Sistem perhitungan pada komputer kuantum ini berbeda dengan komputer digital. Komputer digital melakukan perhitungan secara linier, sedangkan komputer kuantum melakukan semua perhitungan secara bersamaan (karena ada multiple states semua perhitungan dapat berlangsung secara simultan di semua state). Ini berarti ada banyak kemungkinan hasil perhitungan. Untuk mengetahui jawabannya (hasil perhitungannya) kita harus melakukan pengukuran qubit. Tindakan pengukuran qubit ini menghentikan proses perhitungan dan memaksa sistem untuk ‘memilih’ salah satu dari semua kemungkinan jawaban yang ada.

Dengan sistem paralelisme perhitungan ini, kita bisa membayangkan betapa cepatnya komputer kuantum. Komputer digital yang paling canggih saat ini (setara dengan komputer kuantum 40 qubit) memiliki kemampuan untuk mengolah semua data dalam buku telepon di seluruh dunia (untuk menemukan satu nomor telepon tertentu) dalam waktu satu bulan. Jika menggunakan komputer kuantum proses ini hanya memerlukan waktu 27 menit!

Ada satu fenomena ‘aneh’ lain dari mekanika kuantum yang juga dimanfaatkan dalam teknologi komputer kuantum: Entanglement. Jika dua atom mendapatkan gaya tertentu (outside force) kedua atom tersebut bisa masuk pada keadaan ‘entangled’. Atom-atom yang saling terhubungkan dalam entanglement ini akan tetap terhubungkan walaupun jaraknya berjauhan. Analoginya adalah atom-atom tersebut seperti sepasang manusia yang punya ‘telepati’. Jika yang satu dicubit, maka pasangannya (di mana pun ia berada) akan merasa sakit. Perlakuan terhadap salah satu atom mempengaruhi keadaan atom pasangannya. Jika yang satu memiliki spin up (kita baru bisa mengetahuinya setelah melakukan pengukuran) maka kita langsung mengetahui bahwa pasangannya pasti memiliki spin down tanpa kita perlu mengukurnya kembali. Ini melambangkan sistem komunikasi yang super cepat. Komunikasi menggunakan komputer kuantum bisa mencapai kecepatan yang begitu luar biasa karena informasi dari satu tempat ke tempat lain dapat ditransfer secara instant. Begitu cepatnya sehingga terlihat seakan-akan mengalahkan kecepatan cahaya!

Saat ini perkembangan teknologi sudah menghasilkan komputer kuantum sampai 7 qubit, tetapi menurut penelitian dan analisa yang ada, dalam beberapa tahun mendatang teknologi komputer kuantum bisa mencapai 100 qubit. Kita bisa membayangkan betapa cepatnya komputer masa depan nanti. Semua perhitungan yang biasanya butuh waktu berbulan-bulan, bertahun-tahun, bahkan berabad-abad pada akhirnya bisa dilaksanakan hanya dalam hitungan menit saja jika kita menggunakan komputer kuantum yang super canggih dan super cepat itu. Di masa mendatang kita akan menggunakan komputer yang tidak lagi tersusun dari transistor-transistor mini seperti sekarang, Komputer kuantum tidak lagi memerlukan chip komputer yang semakin lama semakin padat karena semakin berlipatgandanya jumlah transistor yang dibutuhkan untuk meningkatkan kinerja komputer. Komputer masa depan justru dipenuhi oleh cairan organik sebagai ‘jantung’nya. Cairan organik ini mengandung atom-atom/partikel-partikel yang bisa berada dalam keadaan superposisi tersebut. Ini berarti, kita benar-benar memanfaatkan zat organik alami untuk menjadi ‘kalkulator’ canggih karena

ternyata cairan organik dari alam memiliki bakat berhitung!